软件设计师
计算机系统知识
CPU的组成
CPU主要由运算器、控制器、寄存器组和内部总线等部件组成
- 运算器
- 算术逻辑单元(ALU):负责处理数据,实现对数据的算术运算和逻辑运算。
- 累加寄存器(AC):也称为累加器,是一个通用寄存器,功能是当运算器的算术逻辑单元执行算术运算或逻辑运算时,为ALU提供一个工作区。
- 数据缓冲寄存器(DR):在对内存储器进行读/写操作时,用DR暂时存放由内存储器读/写的一条指令或一个数据字,将不同时间段内的读/写数据隔离。主要作用是作为CPU和内存、外部设备之间数据传送的中转站;作为CPU和内存、外围设备之间在操作速度上的缓冲;在单累加器结构的运算器中,数据缓冲寄存器还可兼作为操作数据寄存器。
- 状态条件寄存器(PSW):由算数指令和逻辑指令运行或测试的结果建立的各种条件码内容,主要分为状态标志和控制标志
- 控制器
- 指令寄存器(IR):当CPU执行一条指令时,先把它从内存储器取到缓冲寄存器中,再送入IR暂存,指令译码器根据IR的内容产生各种微操作指令,控制其他的组成部件工作,完成所需的功能。
- 程序计数器(PC):存储下一条要执行的指令的地址,具有寄存信息和计数两种功能,又称为指令计数器。程序的执行分为两种情况,一是顺序执行,二是转移执行。
- 地址寄存器(AR):保存当前CPU所访问的内存单元的地址。
- 指令译码器(ID):指令分为操作码和地址码两个部分,为了执行任何给定的命令,必须对操作码进行分析,以便识别所有完成的操作。
- 寄存器组
寄存器组分为专用寄存器和通用寄存器。运算器和控制器中的寄存器是专用寄存器,其作用是固定的。通用寄存器的用途广泛,并且由程序员规定其用途,其数目因处理器的不同有所差异。
指令寄存器(IR)用来保存当前正在执行的指令。当执行一条指令时,先把它从内存取到数据寄存器(DR)中,然后再传送至IR。为了执行任何给定的指令,必须对操作码进行测试,以便识别所要求的操作,指令译码器(ID)就是做这项工作的。指令寄存器中操作码字段的输出就是指令译码器的输入。操作码一经译码后,即可向操作控制器发出具体操作的特定信号。
地址寄存器(AR)用来保存当前CPU所访问的内存单元的地址。由于内存和CPU之间存在着操作速度上的差别,所以必须使用地址寄存器来保持地址信息,直到内存的读/写操作完成为止。
为了保证程序指令能够连续地执行下去,CPU 必须具有某些手段来确定下一条指令的地址,程序计数器正起到这种作用,所以通常又称为指令计数器。在程序开始执行前,必须将它的起始地址,即程序的一条指令所在的内存单元地址送入程序计数器(PC),因此PC的内容即是从内存提取的第一条指令的地址。当执行指令时,CPU将自动修改PC的内容,即每执行一条指令,PC就增加一个量,这个量等于指令所含的字节数,以便使其总保持将要执行的下一条指令的地址。由于大多数指令都是按顺序来执行的,所以修改的过程通常只是简单地对PC加1。
存储系统
- CPU对应的存储类别:寄存器
- Cache对应的存储类别:缓存
- DRAM对应的存储类别:主存
- 硬盘、光盘对应的存储类别:辅存
校验码
奇偶校验码
奇偶校验码(Parity Code)是一种简单有效的校验方法。这种方法通过在编码中增加一位校验位,使编码中1的个数为奇数(奇校验)或偶数(偶校验),从而使码距变为2。海明码
海明码(Hamming Code)是利用奇偶性来查错和纠错的校验方法。海明码确定校验位公式:
$2^k-1 \geq n+k$
$k$:检验位
$n$:数据位
$n+k$:数据总位数校验码在二进制串中的位置为2的整数幂。剩下的位置为数据。如下表所示(以1010110这个二进制数为例):
位置 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 内容 x1 x2 1 x3 0 1 0 x4 1 1 0 为了求出x2,要使所有位置的第二位是1的数据(即形如*1的位置的数据)的异或值为0(不同为1相同为0,结果就是有偶数个1)。即
x2^1^1^0^1^0 = 0。因此x2 = 1。
同理可得x1 = 0, x3 = 1, x4 = 0。位置 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 内容 0 1 1 1 0 1 0 0 1 1 0
循环冗余校验码
循环冗余校验码(Cyclic Redundancy Check,CRC)由两部分组成,左边为信息码(数据),右边为校验码。
输入输出
- 程序控制(查询)方式:分为无条件传送和程序查询方式。方法简单,硬件开销小,但IO能力不 高,严重影响CPU的利用率。
- 程序中断方式:与程序控制方式相比,中断方式因为CPU无需等待而提高了传输请求的响应速度。
- DMA方式:DMA方式是为了在主存与外设之间实现高速、批量数据交换而设置的。DMA方式比程序控制方式与中断方式都高效。
程序设计语言基础知识
后缀式
解决该类问题的方法是将算术表达式构造成一棵二叉树,然后对二叉树进行后序遍历得到后缀式。
a+(b-c)*d的后缀式是abc-d*+
b*(a+c)-d的后缀式是bac+*d-
数据结构与数据运算
树
- 满二叉树:如果一个二叉树的层数为K,结点总数为$2^k-1$个,则它就是满二叉树。
- 完全二叉树:在一个深度为h的完全二叉树中,除第h层外(最后一层),其他各层都是满的。第h层所有的结点都必须从左到右依次放置,不能留空。
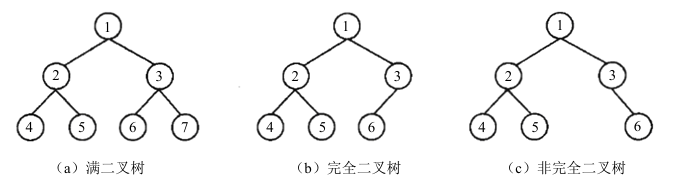
- 最优二叉树:最优二叉树(哈夫曼树)的求法:给出一组权值,将其中两个最小的权值作为叶子节点,其和作为父节点,组成二叉树,而后删除这两个叶子节点权值,并将父节点的值添加到该组权值中。重复进行上述步骤,直至所有权值都被使用完。哈夫曼树节点的度只能是0度或2度。
树转二叉树
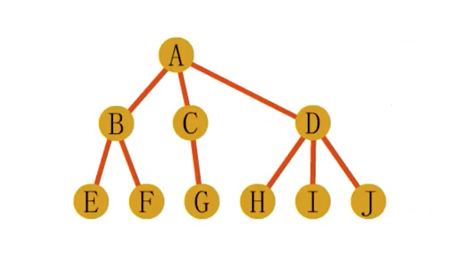
在兄弟结点之间添加连线

去除非长子外的连线
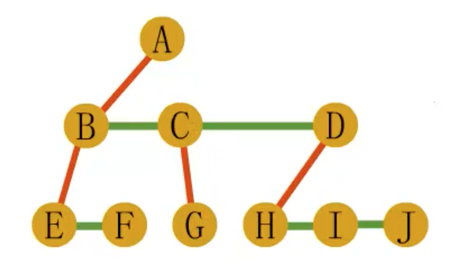
父子连线变为左子树,兄弟连线变为右子树
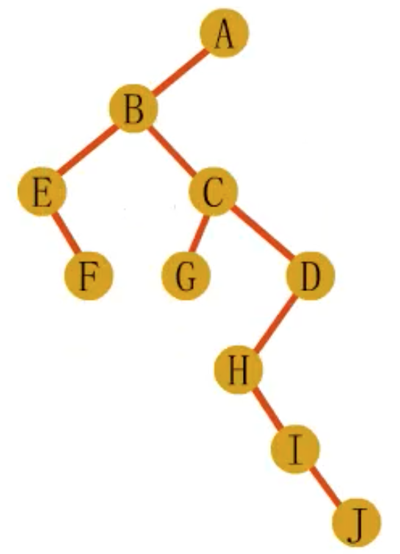
二叉树转树将上述操作反过来即可
图
有向图、无向图以及其邻接矩阵

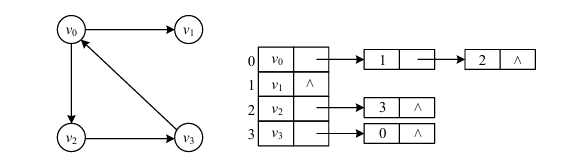
邻接表:邻接表表示法是指为图中的每一个顶点建立一个单链表。
有向图及其邻接表如下图所示
最小生成树
- 最小生成树——克鲁斯卡尔算法:这个算法是从边出发的,因为本质是选取权值最小的n-1 条边,因此,就将边按权值大小排序,依次选取权值最小的边,直至囊括所有节点,要注意,每次选边后要检查不能形成环路。克鲁斯卡尔算法的时间复杂度为O(eloge),与图中的顶点数无关,因此该算法适合于求边稀疏的网的最小生成树。
- 最小生成树——普里姆算法:从任意顶点出发,找出与其邻接的边权值最小的,此时此边的另外一个顶点自动加入树集合中,而后再从这这个树集合的所有顶点中找出与其邻接的边权值最小的,同样此边的另外一个顶点加入树集合中,依次递归,直至图中所有顶点都加入树集合中,此时此树就是该图的最小生成树。普里姆算法的时间复杂度为O(n^2),与图中的边数无关,因此该算法适合于求边稠密的网的最小生成树:
查找
- 顺序查找
将待查的元素从头到尾与表中元素进行比较,如果存在,则返回成功;否则,查找失败。此方法效率不高。顺序查找的平均查找长度为$(n+1)/2$。 - 二分查找
二分查找的前提是元素有序(一般是升序),基本思路是拿中间元素$A[m]$与要查找的元素$x$进行比较,如果相等,则表示找到;如果$A[m]$比$x$大,那么要找的元素一定在$A[m]$前边(左边);如果$A[m]$比$x$小,那么要找的元素一定在$A[m]$后边(右边)。每进行一次查找,数组规模减半。反复将子数组规模减半或使当前子数组为空,直到发现要查找的元素。
长度为$n$的有序数组二分查找的最大查找次数为$\lceil \log_2 n \rceil$(向上取整)。 - 哈希查找
排序
详表
| 排序算法 | 平均 | 最好 | 最坏 | 空间 | 排序方式 | 稳定性 | 备注 |
|---|---|---|---|---|---|---|---|
| 直接插入排序 | $O(n^2)$ | $O(n)$ | $O(n^2)$ | $O(1)$ | In-place | 稳定 | 左侧已排序,右侧未排序,在插入第$i$个记录时,$R_1$,$R_2$,…,$R_{i-1}$均已排好序,这时将第$i$`个记录依次与$R_{i-1}$,…,$R_2$,$R_1$进行比较,找到合适的位置插入,插入位置及之后的记录依次向后移动 |
| 冒泡排序 | $O(n^2)$ | $O(n)$ | $O(n^2)$ | $O(1)$ | In-place | 稳定 | 通过相邻元素($i$ 与 $i-1$)之间的比较和交换,将排序码较小的元素逐渐从底层移向顶层。 |
| 简单选择排序 | $O(n^2)$ | $O(n^2)$ | $O(n^2)$ | $O(1)$ | In-place | 不稳定 | 左侧已排序,右侧未排序,在右侧未排序序列中选择一个最小/最大元素与右侧未排序序列中最左边元素交换 |
| 希尔排序 | $O(n^{1.3})$ | $O(n^{1.3})$ | $O(n^{1.3})$ | $O(1)$ | In-place | 不稳定 | 先将整个序列分为若干子列(由某个增量控制),插入排序子列,减少增量,直至减少为1 |
| 快速排序 | $O(nlog_n)$ | $O(nlog_n)$ | $O(n^2)$ | $O(log_n)$ | In-place | 不稳定 | 使用分而治之思想,选中一个基数(base),比它大的放在右,比它小的放在左,分别在递归排序左右两个序列 |
| 堆排序 | $O(nlog_n)$ | $O(nlog_n)$ | $O(nlog_n)$ | $O(1)$ | In-place | 不稳定 | |
| 归并排序 | $O(nlog_n)$ | $O(nlog_n)$ | $O(nlog_n)$ | $O(n)$ | Out-place | 稳定 |
简图
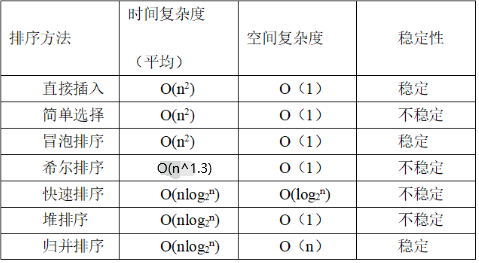
排序算法的稳定性是指在排序过程中,相等元素的相对顺序是否保持不变。如果一个排序算法在排序后,所有相等元素的相对顺序与排序前相同,那么这个排序算法就是稳定的;否则就是不稳定的。
软件工程基础知识
软件过程模型
- 瀑布模型:只适用于需求明确或者二次开发(需求稳定),当需求不明确时,最终开发的项目会错误,有很大的缺陷。
- 瀑布模型的优点:容易理解、成本低、强调开发的阶段性早期计划及需求调查和产品测试。
- 瀑布模型的缺点:缺乏灵活性,客户必须要准确地表达他们的需要;在开始的两个或三个阶段中,很难评估真正的进度状态;项目快结束时,出现大量的集成与测试工作;项目结束之前,不能演示系统的能力。
- V模型:强调测试贯穿项目始终,而不是集中在测试阶段。是一种测试的开发模型。是瀑布模型的一个变体。
- 增量模型:可以有多个可用版本的发布,核心功能往往最先完成,在此基础上,每轮迭代会有新的增量发布, 核心功能可以得到充分测试。强调每一个增量均发布一个可操作的产品。
- 增量模型的优点:可交付的第一个版本所需要的成本和时间很少,开发由增量表示的小系统所承担的风险不大,由于很快发布了第一个版本,因此可减少用户需求的变更。同时,它也具有瀑布模型所有的优点。
- 增量模型的缺点:若没有对用户的变更要求进行规划,那么产生的初始增量可能会造成后来增量的不稳定;若需求不像早期思考的那样稳定和完整,那么一些增量就可能需要重新开发或重新发布;管理发生的成本、进度和配置的复杂性可能会超出组织的能力。
- 演化模型(原型模型、螺旋模型):典型的演化模型有原型模型和螺旋模型。
- 原型模型:典型的原型开发方法模型。适用于需求不明确的场景,可以帮助用户明确需求。
- 螺旋模型:结合了瀑布模型和演化模型的优点,但是增加了风险分析,针对需求不明确的项目,这也是其最大的特点。适合大型项目开发。
- 喷泉模型:以用户需求为动力,以对象为驱动,适合于面向对象的开发方法
- 基于构件的开发模型:基于构件的开发模型是指利用预先包装的构件来构造应用系统。构件可以是组织内部开发的构件,也可以是商品化成品(COTS)软件构件。一种基于构件的开发模型包括领域工程和应用系统工程。
- 形式化方法模型:形式化方法是建立在严格数学基础上的一种软件开发方法,主要活动是生成计算机软件形式化的数学规格说明。
- 统一过程模型:统一过程(UP)模型是一种“用例和风险驱动,以架构为中心,迭代并增量”的开发过程,由UML方法和工具支持。
- 统一过程的典型代表是RUP,RUP是UP的商业扩展,完全兼容UP,比UP更完整、更详细。
- 敏捷方法的总体目标是通过“尽可能早地、持续地对有价值的软件进行交付”使客户满意。敏捷过程的典型方法有很多,每一种方法基于一套原则,这些原则实现了敏捷方法所宣称的理念,即敏捷宣言。
- 常用的方法:极限编程(XP)、水晶法(Crystal)、并列争球法(Scrum)、自适应软件开发(ASD)、敏捷统一过程(AUP)。
软件的四个维护方面
- 改正性维护是指改正在系统开发阶段已发生而系统测试阶段尚未发现的错误。
- 适应性维护是指使应用软件适应信息技术变化和管理需求变化而进行的修改。
- 完善性维护是指为了扩充功能和改善性能而进行的修改,主要是指对已有的软件系统增加一些在系统分析和设计阶段中没有规定的功能与性能特征。
- 预防性维护是指为了改进应用软件的可靠性和可维护性,为了适应未来的软件、硬件环境的变化,应主动增加预防性的新功能,以使应用系统可以适应各类变化而不被淘汰。
结构化开发方法
结构化分析方法
结构化分析(SA)概述
抽象(自底向上)、分解(自顶向下)
数据流图(DFD)的基本要素:外部实体、加工、数据存储、数据流
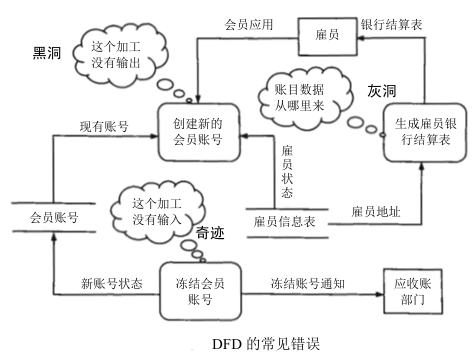
数据流图的常见错误
数据流图的审查
- 一致性:父图与子图平衡、数据守恒、具备数据存储、输出不能与输入同名。
- 完整性:奇迹(无入有出)、黑洞(有入无出)、灰洞(无法出)。
结构化设计方法
- 模块结构图是结构化设计的工具,由模块、调用、数据、控制和转接五种基本符号组成。
- 结构化设计主要包括:体系结构设计、数据设计、接口设计、过程设计。
面向对象技术
面向对象测试
面向对象测试分为四个层次执行:
- 算法层:测试类中定义的每个方法,基本相当于传统软件测试的单元测试。
- 类层:测试封装在同一个类中的所有方法与属性之间的相互作用。可以认为是面向对象测试中特有的模块测试。
- 模板层:测试一组协调工作的类之间的相互作用。大体上相当于传统软件测试中的集成测试。
- 系统层:把各个子系统组装成完整的面向对象软件系统,在组装过程中同时进行测试。
UML的关系
UML中有四种关系:依赖、关联、泛化和实现
- 依赖关系:一个事物发生变化影响另一个事物。
- 关联关系:描述了一组链,链是对象之间的连接。
- 泛化关系:特殊/一般关系。
- 实现关系:接口与类之间的关系。
- 聚合关系:整体与部分生命周期不同。
- 组合关系:整体与部分生命周期相同。
设计原则
- 稳定抽象原则:此原则强调的是包的抽象程度与其稳定程度一致。
- 稳定依赖原则:此原则要求包之间的依赖关系都应该是稳定方向依赖的,即包要依赖的包要比自己更具有稳定性。
- 依赖倒置原则:此原则强调的是程序应该依赖于抽象接口,而不是具体的实现,从而降低客户与实现模块间的耦合。
- 无环依赖:这个原则明确指出,在组件的依赖关系在图中不允许存在环。
设计模式
创建型设计模式
抽象工厂(Abstract Factory)
提供一个接口,用于创建相关或依赖对象的家族,而无需明确指定具体类。
应用场景:需要创建一组相关或相互依赖的对象时,例如跨平台 UI 工具包。生成器(Builder)
将一个复杂对象的构建过程与其表示分离,使得同样的构建过程可以创建不同的表示。
应用场景:需要创建复杂对象,并且需要灵活地控制其构建过程时,例如构建器模式用于生成复杂的文档或报表。工厂方法(Factory Method)
定义一个用于创建对象的接口,让子类决定实例化哪一个类。
应用场景:当一个类无法预知它需要创建的对象时,例如日志记录器可以根据配置选择不同的日志记录方式。原型(Prototype)
通过复制现有对象来创建新对象,而不是通过实例化类。
应用场景:需要大量相似对象时,例如克隆复杂对象以提高性能。单例(Singleton)
确保一个类只有一个实例,并提供一个全局访问点。
应用场景:需要全局唯一的对象时,例如配置管理器、线程池或数据库连接池。
结构型设计模式
适配器(Adapter)
将一个类的接口转换成客户希望的另一个接口,使得原本由于接口不兼容而不能一起工作的类可以协同工作。
应用场景:系统需要使用现有的类,但其接口不符合需求时,例如将旧系统的接口适配到新系统。桥接(Bridge)
将抽象部分与实现部分分离,使它们可以独立变化。
应用场景:需要在抽象和实现之间增加更多的灵活性时,例如跨平台图形界面工具。组合(Composite)
将对象组合成树形结构以表示“部分-整体”的层次结构,使得客户端可以统一地处理单个对象和组合对象。
应用场景:需要表示对象的部分-整体层次结构时,例如文件系统中的文件和文件夹。装饰(Decorator)
动态地给对象添加一些额外的职责,而不影响其他对象的功能。
应用场景:需要动态地扩展对象的功能时,例如为图形界面组件添加滚动条或边框。外观(Facade)
为子系统中的一组接口提供一个一致的界面,使得子系统更容易使用。
应用场景:需要为复杂的子系统提供一个简单的接口时,例如为多模块系统提供统一的入口。享元(Flyweight)
运用共享技术有效地支持大量细粒度对象的复用,减少内存消耗。
应用场景:需要大量相似对象时,例如字符处理系统中的字符对象。代理(Proxy)
为其他对象提供一种代理以控制对这个对象的访问。
应用场景:需要控制对对象的访问时,例如远程代理、虚拟代理或保护代理。
行为设计模式
责任链(Chain of Responsibility)
允许多个对象有机会处理请求,将这些对象连成一条链,沿着链传递请求,直到某个对象处理它为止。
应用场景:日志处理、权限校验等。命令(Command)
将请求封装为对象,使得可以用不同的请求、队列或日志来参数化对象。支持撤销和重做操作。
应用场景:事务操作、按钮点击事件处理。解释器(Interpreter)
定义一种语言的文法表示,并提供一个解释器来解释语言中的句子。
应用场景:编译器、正则表达式解析器。迭代器(Iterator)
提供一种方法顺序访问集合对象中的元素,而不暴露其内部表示。
应用场景:遍历集合(如数组、链表)。中介者(Mediator)
用一个中介对象封装一组对象之间的交互,使对象之间不需要直接引用,降低耦合性。
应用场景:聊天室、MVC 中的控制器。备忘录(Memento)
在不破坏封装的前提下,捕获对象的内部状态,并在以后恢复它。
应用场景:撤销功能、游戏存档。观察者(Observer)
定义对象间的一对多依赖关系,当一个对象状态改变时,所有依赖它的对象都会收到通知并自动更新。
应用场景:事件监听、发布-订阅模式。状态(State)
允许对象在内部状态改变时改变其行为,看起来像是改变了其类。
应用场景:状态机、订单状态管理。策略(Strategy)
定义一系列算法,将每个算法封装起来,并使它们可以互换。
应用场景:支付方式选择、排序算法。模板方法(Template Method)
定义一个操作的骨架,将一些步骤延迟到子类中。子类可以不改变骨架的情况下重新定义某些步骤。
应用场景:算法框架、代码生成器。访问者(Visitor)
提供一种操作一组对象的方法,使得可以在不改变这些对象的类的前提下定义新的操作。
应用场景:编译器语法树操作、对象结构遍历。
算法设计与分析
分治法
基本思想
使用递归技术,把一个问题拆分成多个小规模的相同子问题。
实例:归并排序、快速排序、二分搜索
动态规划法
基本思想
- 找出最优解的性质,并刻画其结构特征。
- 递归定义最优解的值。
- 自底向上算出最优解。
- 构造最优解。
实例:矩阵乘法、背包问题、LCS最长公共子序列
贪心法
一般用于求满意解,特殊情况可求最优解(部分背包)
实例:背包问题(如装箱)、多机调度、找零钱问题
回溯法
系统地搜索一个问题的所有解或任一解。有试探和回退的过程。
实例:N皇后问题、迷宫、背包 问题
数据库技术基础
关系数据库的规范化
Armstrong公理
Armstrong公理系统设关系模式R<U,F>,其中U为属性集,F是U上的一组函数依赖,那么有如下推理规则:
A1自反律:若Y⊆X⊆U,则X→Y为F所蕴含;
A2增广律:若X→Y为F所蕴含,且Z⊆U,则XZ→YZ为F所蕴含;
A3传递律:若X→Y,Y→Z为F所蕴含,则X→Z为F所蕴含。
根据上面三条推理规则,又可推出下面三条推理规则:
合并规则:若X→Y,X→Z,则X→YZ为F所蕴含。
分解规则:若X→Y,Z⊆Y,则X→Z为F所蕴含。
伪传递规则:若X→Y,WY→Z,则XW→Z为F所蕴含。
数据库操作
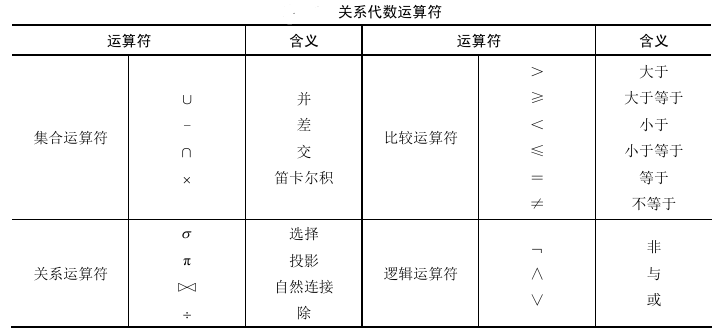
基本关系运算
- 笛卡尔积:相乘。
- 投影π:选列。
- 选择σ:选行。
- 自然连接~:结果的属性列数是二者之和减去重复列数,结果元组是同名属性列取值相等的元组。
关系数据库的规范化

权限
- GRANT:授权
- REVOKE:撤权
网络与信息安全基础知识
网络体系结构
| 层次 | 名称 | 主要功能 | 主要设备及协议 |
|---|---|---|---|
| 7 | 应用层 | 实现具体的应用功能 | POP3、FTP、HTTP、Telnet、SMTP、DHCP、TFTP、SNMP、DNS |
| 6 | 表示层 | 数据的格式与表达、加密、压缩 | 同应用层 ↑ |
| 5 | 会话层 | 建立、管理和终止会话 | 同应用层 ↑ |
| 4 | 传输层 | 端到端的连接(端口) | TCP、UDP |
| 3 | 网络层 | 分组传输和路由选择(IP) | 三层交换机、路由器、ARP、RARP、IP、ICMP、IGMP |
| 2 | 数据链路层 | 传送以帧为单位的信息(MAC) | 网桥、交换机、网卡、PPPT、L2TP、SLIP、PPP |
| 1 | 物理层 | 二进制传输(01) | 中继器、集线器 |
未分类
关键路径
项目软件活动图中,关键路径指的是从开始到结束最长的一条路径
沟通路径
$$
C=n(n-1)/2
$$
n:团队成员数量
C:沟通路径条数
树的度、叶子节点数、边数
问:
对于一棵树,每个结点的孩子个数称为结点的度,结点度数的最大值成为树的度。某树T的度为4,其中有5个度为4的结点,8个度为3的结点,6个度为2的结点,10个度为1的结点,则T中的叶子结点个数为?
解:
设度为0的叶子结点数为$n_0$,度为1的结点数为$n_1$,度为2的结点数为$n_2$,度为3的结点数是$n_3$,度为4的结点数为$n_4$
$n_1=10$
$n_2=6$
$n_3=8$
$n_4=5$
这里有一个公式
$边的总数=结点总数-1$
度数为n的节点会向下产生n条边,那么就有
$4n_4+3n_3+2n_2+n_1=n_0+n_1+n_2+n_3+n_4-1$
$20+24+12+10=n_0+29-1$
$n_0=38$
因此叶子结点个数为38
常见协议功能和默认端口
| 协议名 | 默认端口 | 功能 | 特殊说明 |
|---|---|---|---|
| HTTP | 80 | 超文本传输协议,网页传输 | 不安全,结合SSL的HTTPS协议是安全的超文本传输协议,默认端口443 |
| Telnet | 23 | 远程协议 | 不安全,SSH是安全的远程协议 |
| FTP | 20数据 21控制 | 文件传输协议 | 不安全,结合SSL的SFTP是安全的文件传输协议。 |
| POP3 | 110 | 邮件收取 | 附加多媒体数据时需采用MIME(MIME不安全,结合SSL的MIME/S是安全的多媒体邮件协议)。使用WEB方式收发电子邮件时必须设置账号密码登录。 |
| SMTP | 25 | 邮件发送 | |
| DNS | 53 | 域名解析协议,记录域名与IP的映射关系 | 本地客户端主机首查本机hosts文件 域名服务器首查本地缓存 |
| DHCP | 67 | IP 地址自动分配 | 169.254.X.X 和 0.0.0.0 是无效地址 |
| SNMP | 161 | 简单网络管理协议 | 服务器仅发送消息给当前团体 |
| ARP | 地址解析协议,IP 地址转换为 MAC 地址 | ARP Request 请求采用广播进行传送 ARP Response 响应采用单播进行传送 | |
| RARP | 反向地址解析协议,MAC 地址转 IP 地址 | 无 | |
| ICMP | 因特网控制协议 | PING 命令来自该协议 | |
| IGMP | 组播协议 | 无 |
常见算法
- Hash算法
- SHA
- 对称加密算法
- DES
- IDEA
- 非对称加密算法
- RSA
可靠度
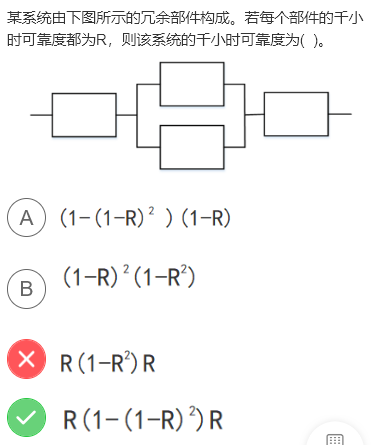
- 串联的可靠度位每个部件相乘
- 并联的可靠度为$(1-(1-R)^n)$
其中$(1-R)$为单个组件的不可靠度,并联的总体不可靠度为单个组件的不可靠度的乘积$(1-R)^n$,因此总体的可靠度为$(1-(1-R)^n)$
数据库安全相关术语
- 拖库: 本是数据库领域的专用术语,指从数据库中导出数据。现指网站遭到入侵后,黑客窃取数据库的行为,即数据库信息泄露。
- 撞库: 使用大量从一个网站获取的账号密码,尝试登录另一个网站。基于用户密码复用率较高的问题,利用泄露的密码尝试其他网站。
- 洗库: 黑客入侵网站后获取大量用户数据,通过技术手段和黑色产业链将有价值的数据变现。
- 社工库: 黑客将获取的各种数据库关联起来,对用户进行全方位画像。
软件测试方法
- 语句覆盖:每个语句至少执行一次(进每个房间)。
- 分支覆盖:每个条件的每个分支至少执行一次(开关每扇门)。
- 判定覆盖:每个条件的每个布尔值(True/False)至少执行一次(测试灯的开关)。
- 路径覆盖:每条可能的路径至少执行一次(探索迷宫中的每条路径)。
程序流程图
McCabe复杂度
- 语句覆盖(Sstatement Coverage):也称为行覆盖,它关注的是程序中每一行代码是否至少被执行一次。这是最基本的测试爱盖标准,但往往只能发现简单的错误。
- 判定覆盖(Decision Coverage):也称为分支覆盖,它要求程序中的每一个判定(例if-else语句)的每一种可能古果(真或假)都至少发生一次。这比语句夏盖更全面,但可能会逮漏一些错误。
- 条件硬盖(Condtioncoverage):它要求程序中的每一个条件(例如语句中的条件)的每一种可能结果(真或假)都至少发生一次。虽然这比判定要盖更全面,但它仍然可能患漏一些错误,因为它不保证所有条件的组合都被测试到。
- 路径硬盖(Patn Coverage):它要求测试瘦盖程序中所有可能的执行路径。这通常意味着测试需要遍历程序中所有可能的条件组合。路经覆善是这些法项中最全面的测试覆盖方法,因为它考虑了程序中所有可能的执行路径。
测试
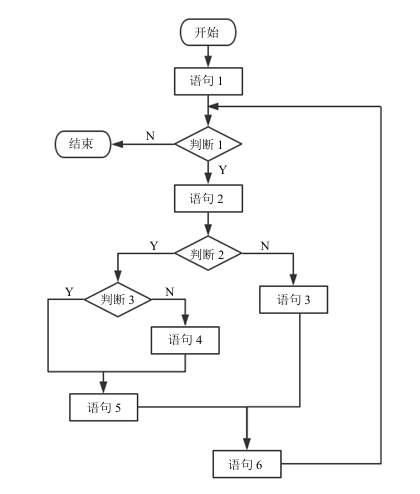
语句覆盖:2
路径覆盖:4
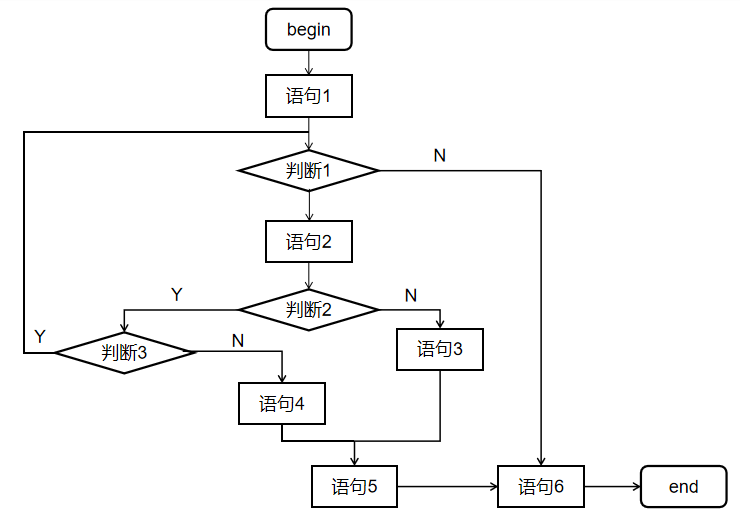
路径覆盖:6
流水线技术
- 流水线建立时间:第1条指令执行时间。
- 流水线周期:指令分段后,最长段时间。
- 流水线执行时间:流水线总+(指令条数- 1)*流水线周期。
- 吞吐率=指令条数/流水线执行时间。
- 最大吞吐率=流水线周期的倒数。
UML序列图
loop循环
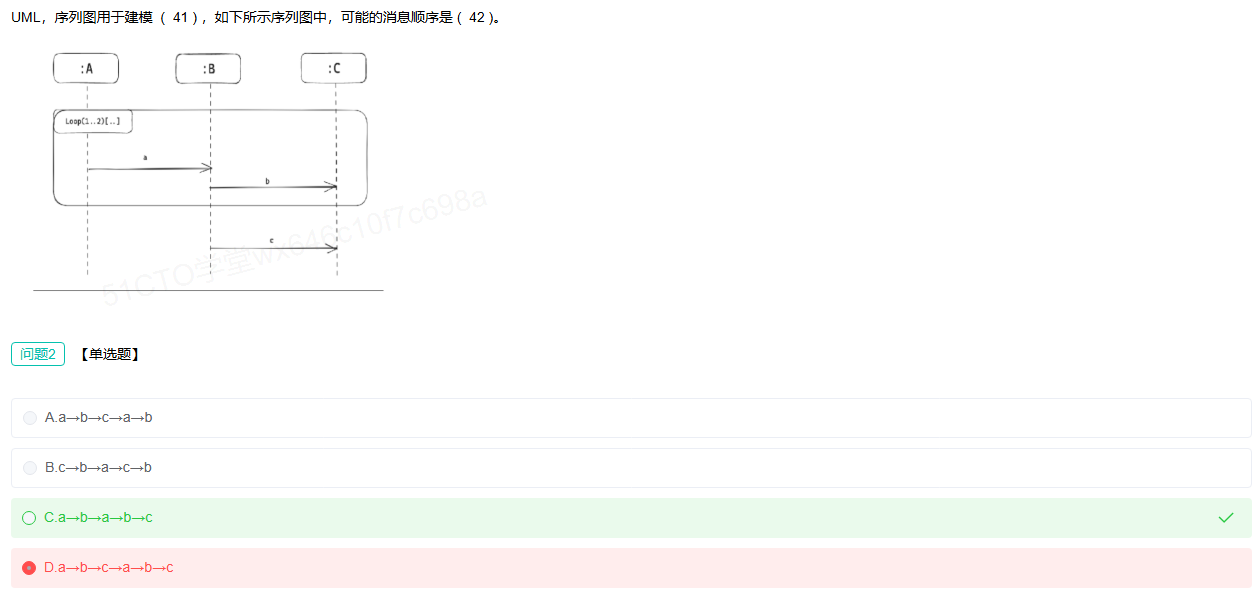
文件系统索引

第一问:地址直接访问和一级间接地址访问
第二问解答:
$1kb/4b=256$
直接索引地址:$5*(256^0)=5$
一级间接地址索引:$2*(256^1)=512$
二级间接地址索引:$1*(256^2)=2^{16}$
$5+512+2^{16}=66053$
第二问答案:66053
页式存储管理系统

0对应的是2
$2*4k=8k=8192$

逻辑地址8644对应的页号是2(8644/4k,取2余452)
因此位于第2页452处,也就是第8块452处
$8*4k+452=33220$
因此答案是33220
.png)

