.png)
原码、反码、补码、移码
原码、反码、补码、移码
原码、反码、补码和移码是计算机中表示和处理有符号数的几种方法。
原码
原码是计算机中表示有符号数的一种最简单的方法。它使用最高位表示符号位，0表示正数，1表示负数，其余位表示数值的绝对值。例如，8位二进制数中，+5的原码表示为00000101，-5的原码表示为10000101。
表示范围：8位原码的表示范围为[-127~+127]
反码
反码是对原码的一种改进表示方法。正数的反码与原码相同，负数的反码是对原码逐位取反（符号位除外）。例如，8位二进制数中，+5的反码表示为00000101，-5的反码表示为11111010。
表示范围：8位反码的表示范围为[-127~+127]
补码
补码是计算机中最常用的表示有符号数的方法，常用于进行数字加减法。正数的补码与原码相同，负数的补码是其反码加1。例如，8位二进制数中，+5的补码表示为00000101，-5的补码表示为11111011。
表示范围：8位补码的表示范围为[-128~+127]
下表为4位补码与十进制的对应关系
| 补码 | 十进制 |
|---|---|
| 0111 | 7 |
| 0110 | 6 |
| … | … |
| 0010 | 2 |
| 0001 | 1 |
| 0000 | 0 |
| 1111 | −1 |
| 1110 | −2 |
| … | … |
| 1001 | −7 |
| 1000 | −8 |
以4位补码为例，可以将补码理解为在原数字的基础上进行了偏移处理的结果。补码的范围是0~15，而原数字的范围是-8~7。具体来说：
- 对于
0和正数，补码的值与原数字相同，范围为0~7。 - 对于负数，补码的值是从最大值
15开始向0偏移，范围为15~8。例如，-1的补码为15，-2的补码为14，依此类推，直到-8的补码为8。
补码可以简化有符号整数的加减法运算，将其都统一成补码的加法运算
1 | 0011 (3) |
移码
移码通常用于表示浮点运算的阶码。无论正数负数，都是将该原码的补码的首位(符号位) 取反得到移码。例如，假设使用8位移码，则+5的移码表示为10000101，-5的移码表示为01111011。
在数轴上，移码所表示的范围，恰好对应于真值在数轴上的范围向正方向移动${2^{n}}$个单元
补码表示的好处在于去掉了负号，但人们很难从形式上判断真值大小，与人们的习惯不符;因为补码表示中符号也成了一位二进制的数，而移码的表示中与补码相差一个符号位，而且可以从移码看出真值的大小，转换方便。
| 补码 | 移码 | 十进制 |
|---|---|---|
| 0111 | 1111 | 7 |
| 0110 | 1110 | 6 |
| … | … | … |
| 0010 | 1010 | 2 |
| 0001 | 1001 | 1 |
| 0000 | 1000 | 0 |
| 1111 | 0111 | −1 |
| 1110 | 0110 | −2 |
| … | … | … |
| 1001 | 0001 | −7 |
| 1000 | 0000 | −8 |
0的原码、反码、补码、移码
| 原码 | 反码 | 补码 | 移码 | |
|---|---|---|---|---|
| +0 | 00000000 | 00000000 | 00000000 | 10000000 |
| -0 | 10000000 | 11111111 | 00000000 | 10000000 |
浮点数的二进制表示
下面以半精度浮点数为例
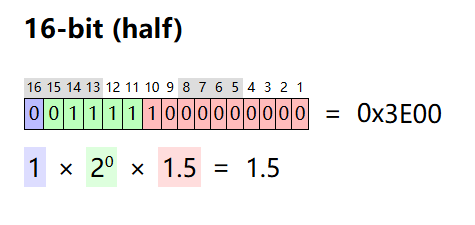
半精度浮点数的二进制表示主要包含：符号位(16)、指数位(15-11)、尾数(10-1)
- 符号位：浮点数的正负
- 指数位：表示浮点数的指数部分（采用偏移法表示）
- 尾数：表示浮点数的精确值
浮点数加法运算
- 首先先进性对阶，阶码小的向阶码大的对齐，同时尾数进行右移（变小）。
- 然后再对尾数进行加减法运算。
- 然后进行规格化处理（IEEE754）。
TODO
- 浮点数的规格化
